Recently there is mounting interest in buying gold (for example, see this report at TheStreet.com). I am not much of a fundamental analyst, so I won’t go into the economic reasons whether to own or not own gold now. Rather, I would like to see if there is an arbitrage opportunity here in the midst of all this excitement.
I talked about before why I believe energy futures and energy companies ETF are “cointegrated”, i.e. when their spread wanders far from a mean value, there is a high probability that they will revert to the mean. The same analysis can be made about other pairs of commodity futures and ETF’s. Therefore I apply this to gold.
Looking around for ETF’s that hold gold miners, I found GDX. It started trading on May 23, 2006 and therefore has a relatively short history for us to analyze. We could have paired it against the front-month gold futures contract GC, but this may be inconvenient because one has to rollover the contracts monthly. So instead, we pair it against an ETF that holds gold as a commodity. GLD is one such example. (So is IAU, but GLD is far more liquid.) Using the same Matlab cointegration package that I mentioned in the previous article, I determine that even with the short history, GLD cointegrates with GDX with a 90% probability. Also, the package tells us the proper combination is 60 shares of GLD vs. 100 shares of GDX. So if we form a pair by buying 60 shares of GLD and shorting 100 shares of GDX, we can plot the value over time here:
I talked about before why I believe energy futures and energy companies ETF are “cointegrated”, i.e. when their spread wanders far from a mean value, there is a high probability that they will revert to the mean. The same analysis can be made about other pairs of commodity futures and ETF’s. Therefore I apply this to gold.
Looking around for ETF’s that hold gold miners, I found GDX. It started trading on May 23, 2006 and therefore has a relatively short history for us to analyze. We could have paired it against the front-month gold futures contract GC, but this may be inconvenient because one has to rollover the contracts monthly. So instead, we pair it against an ETF that holds gold as a commodity. GLD is one such example. (So is IAU, but GLD is far more liquid.) Using the same Matlab cointegration package that I mentioned in the previous article, I determine that even with the short history, GLD cointegrates with GDX with a 90% probability. Also, the package tells us the proper combination is 60 shares of GLD vs. 100 shares of GDX. So if we form a pair by buying 60 shares of GLD and shorting 100 shares of GDX, we can plot the value over time here:
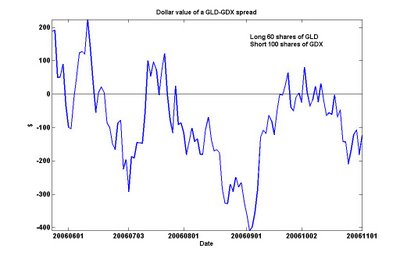
There are some caveats with trading this spread. First, it is not always easy to borrow GDX or GLD to short. It depends on if your broker has a good securities lending desk. Secondly, the history of GDX is short. So any analysis must be taken with a grain of salt. To overcome this short history, I could have constructed my own basket of gold mining stocks and plot the price of this basket against the gold futures GC. If you intend to invest heavily into this spread, I would definitely recommend doing this piece of hard work.
16 comments:
EC-
A similar opportunity could be found in the new CME derivatives for housing and housing stocks. the housing derivatives are fairly new so adoption hasn't been very quick, but slowly it's going to come and then similar arbitrage opportunities could be found.
What do you think about pairing lumber futures with housing stocks?
Yaser: thanks for these great ideas! I will look into them and do some analysis in the next while and post them here. -EC
Mr. Chan,
I recently came upon your site, which is quite interesting. Thank you.
Have you revisited the Gold vs. Gold miner arbitrage? Has the relationship changed? It behaved well until last summer/fall. How would you have handled that? Thanks for your thoughts.
dk,
Yes, it had been a rough year for this pair. But inevitably, some pairs fall out of line for a long time (a year?) and then come back, others will never converge. The key is to divide the capital among many pairs so each one cannot do too much damage.
Ernie
Hey Ernie,
I just read your book and I gained some valuable insight into developing my own trading strategies. In fact I modified matlab script published in your book to download daily price data on the S&P500, then perform cointegration tests for every stock against the other stocks in their sector. I am now working on developing a script that will help me identify which pairs have a shorter mean holding time. Can you give me any advice? Maybe you have published some code that I didn't see or are willing to share? Keep up the good work.
Ryan
Hi Ryan,
Example 7.5 in my book has sample code on how to calculate half-life for mean-reversion.
Ernie
Hi, I have recently read your book, and I have some questions, how did you figure that we need to go long 60 shares and short 100shares with GLD,GDX using MatLab?
Thank you,
Julian
Hi Julian,
I regress GLD's against GDX's prices.
The regression coefficient determines the hedge ratio.
Ernie
EC - I just bought your book and was interested in the recent (last 3 months) history of the GDX-GLD spread. The current data (10/7/2010) shows a z score of 10.46.
Is that 10+ standard deviations? How long has it been in a 3+ standard deviation range?.......Tom Mc
Hi Tom,
You must be referring to the z-score for GDX-GLD as shown on http://epchan.com/subscription/spread.htm.
Indeed, this spread has wandered very far from its original mean since 2006. However, if you trade this spread using the Bollinger band approach, you would be updating the mean and SD regularly.
The purpose of my web page is to show that some spreads do wander away, and is not really cointegrating, but others, like EWC-EWA, do remain cointegrating out-of-sample.
Ernie
Hi Ernie,
I just wanted to share with your readers my implementation of the gld/gdx arb on quantopian: https://app.quantopian.com/posts/ernie-chans-gold-vs-gold-miners-stat-arb
thanks,
fawce
This pair recently gone to the new low !
Seems that between 2007 and 2014 the GLD and GDX were not really co-integrated well. Interestingly, since the beginning of 2014, they are again co-integrated nicely - see the gray line being (GLD$AdjClose - GDX$AdjClose) in https://www.dropbox.com/s/yk31rccgza0470k/GDX_vs_GLD.png?dl=0
Hi Jaroslav,
Yes, pairs do come in and out of cointegration. Trick is how to prevent too steep a drawdown while they are out.
Ernie
When doing linear regression to figure out the hedge ratio what does it mean if the residuals are stationary but end up looking like the price time series of y. Do I still trade on y ~ x or should I look for another combination?
Use orthogonal, or Deming, regression instead of OLS.
Post a Comment