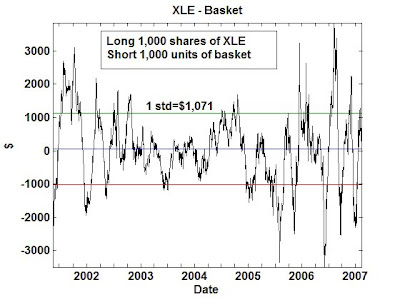
XLE is composed of some 33 stocks (as of 2/16/2007). Our goal is to pick some smaller subset of these stocks to form a basket. We pick them based on how well they cointegrate with XLE. How big should this subset be? The higher the number, the better this basket cointegrates with XLE, but the smaller the profits. (If you include all stocks in XLE in this basket, then the basket cointegrates perfectly with XLE, but there will be no trading opportunities!) The lower the number, the higher the (specific) risk as well as return. So it is more of a personal risk-return preference than any scientific criterion which determines how many stocks to pick. I pick a basket with 10 stocks. I have found that this basket cointegrates with XLE with better than 99% probability since 2001/05/22. The half-life for mean-reversion is about 20 days, which means you have to hold a position for at most a quarter. (My own rule is to exit when the spread hasn't reverted in 3 times the half-life.) If you enter into a position when the z-score is about ±2, you can expect a profit of about $2,000 on an investment of about $58,000 on one side. This comes to a return per trade of about 3%. You can of course boost this return by using options to implement the XLE position instead.
As an aside, if you use Interactive Brokers, you can easily trade an entire basket of stocks using their Basket Trader.
I have created an online spreadsheet with (almost) real-time values of this spread in the subscription area. (The detailed composition of this basket of 10 stocks are also described there.) Note that in theory, every time the XLE changes composition, we will have to re-compute our basket composition as well. But fortunately XLE composition does not change very much or very often, so I will only update my basket at most once a month.
41 comments:
Ernest
I really enjoy reading your blog...I would like to know if there are any programs you are aware of where I can find co-integration properties between baskets of stocks (ie - Insurance stocks, Homebuilders)..I am looking to trade WITHIN basets of stocks (ie - track 6 homebuilders and be long 1 or 2 and short 1 or 2 at any given time)
You can reach me directly at Ysettle@earthlink.net if you have any ideas
Neil
Ernest
I really enjoy reading your blog...I would like to know if there are any programs you are aware of where I can find co-integration properties between baskets of stocks (ie - Insurance stocks, Homebuilders)..I am looking to trade WITHIN basets of stocks (ie - track 6 homebuilders and be long 1 or 2 and short 1 or 2 at any given time)
You can reach me directly at Ysettle@earthlink.net if you have any ideas
Neil
First, thanks for these 2 great little explanations of a cointegration trade.
cointegration-is-not-same-as.html
gold-vs-gold-miners-another-arbitrage.html
> you can expect a profit of about $2,000 on an investment of about $58,000 on one side.
Next, excuse the following newbie question.
Q: Is the % return really just 3% ? Can't the short sale proceeds finance the long position? If so, is the "basis" just what the margin req. is? Can this trade theoretically go infinite? (More shorts finance more longs). Is the margin req. the real basis in calc'ing the % return?
Lastly, to recap, the point is this trade is simply to arbitrage the "temp" divergence of the 10 basket stocks with their underlying index?
Dear Anonymous,
Your are correct in saying that the real return of this trade is based on how much leverage you can get. If you are in a hedge fund or has a prop trading account somewhere, you may get many more times leverage than the retail trading account for this kind of hedged trade. One must consider, however, the potential maxmimum drawdown, even if you have infinite leverage, as that can wipe out equity.
Your summary of the essence of this trade is also correct. The temporary divergence is what we want to trade on.
Thank you for your questions!
Ernie
...so with NO leverage, based on the long position of $58k, the $2k profit is ~ 3.4%. (Anything return beyond that is up to the reader, but is not "counted" as the base return)
Ernest,
Doesn't your idea have a fundamental flaw? The index consists of a relatively small number of stocks. The error process that is the difference between the index and any "cointegrating" basket made out of the same components is basically a (weighted) sum of the components not included in the basket.
There is no reason to believe that this error process will be stationary (and hence the cointegration will be genuine), because it will be a sum of relatively few price processes each of them basically doing the random walk. A sum of a small number of random walks can'be expected to be very mean reverting in general.
As an example, consider the limit when, as you say, the cointegration is very "good": for an index of N components you have included N-1 components in your basket. Now, this basket will approximate the index very well indeed. However, the difference (index - basket) is the one component left out and it is manifestly not mean reverting (being a process corresponding to a single stock). If that Nth component were mean reverting, we would just trade it directly and not bother with the synthetic hedge...
Dear Anonymous,
Thank you for your thought-provoking comment. Let's focus on the N-1 example you gave. I believe the way to resolve this apparent paradox is to look at the relative weight of the N-1 stocks vs the 1 stock within the index XLE. Intuitively speaking, if the total weight of the N-1 stocks is 99.999%, whereas the weight of the 1 stock is just 0.001%, and assuming the volatilities of the stocks are about the same, it will take very very long before this small amount of random walk to affect our cointegration relationship. Of course, the weight of our excluded stocks is not so negligible, but any error is reflected in the t-statistic calculated for the cointegration relationship. If the weight of the excluded stocks is high enough, the t-statistic will show the likelihood of cointegration to be low. Let me know what you think of this argument!
Ernie
Ernie,
Thanks for responding. Continuing with this cointegration thread (I will identify myself as "L" in this and future posts):
1. I did not quite follow your t-statistic argument -- perhaps I need more details about your approach to finding cointegration to know which parameter you apply this statistic to.
I am familiar with Engle-Granger and Jonansen approaches. Which one do you use and how do you validate its out-of-sample performance? If you try any of them on an index with small N, it is easy to verify that both of them will basically recover the index component structure, giving us what we already know -- that the full N basket with the weights as set by the index design is the best cointegrating vector :)
2. The following thought goes to the heart of this matter, I think: what are the fundamental underlying reasons for cointegration to exist?
In traditional econometric examples, components share common stochastic trends. For example, supply and demand cointegrate for obvious reasons -- roughly speaking, what's available will be consumed sooner or later, athough the individual steps will be pretty stochastics. Simple, but fundamental -- and hence not spurious.
But what is the fundamental reason for cointegration to exist between an index and a basket of components? Unfortunately, there is nothing except the fact that the an index share, if it is small and tradeable (HOLDR, SPDR), represents precise mathematical ownership of all of the components with some known weights. There are no other supply/demand, etc fundamental reasons. There are market participants making sure that no riskless arbitrage opportunities exists between the index and its components -- and the only relevant relationship here is that mathematical set of weights that comprise the index.
3. It seems to me that attempting to find cointegration between the index and a small subset of N will *likely* result in what I would call "spurious cointegration". It (and all relevant t-statistics, etc) will look quite good in-sample, but will vanish very quickly out of sample. Regressing stock prices on each other (like in Engle-Granger) is good at inducing in-sample cointegration for any random collection of stocks :)
I believe your blog at some point linked to a paper by Dunie and Ho, "Cointegration portfolios of European equities for index tracking and market neutral strategies". It may not be a coincidence that the authors used a simple heuristics for stock selection: they pick stocks with the larger weight in the index first. It is easy to verify that this "heuristic" works well -- but that's because it's a greedy way to approach the ideal limit of all N stocks in the basket.
What I am basically driving at is that it's not a paradox -- I just don't think that the idea works in the first place. But you are welcome to prove me wrong with some out-of-sample analysis.
Cointegration is not spurious when there is genuine cancellation of common stochastic trends. If you start with a small set of N instruments, then by luck there may be some linear combinations of instruments that cancel out these trends -- but why one of these instruments needs to be the index itself I just don't see? A index over small N has all of the individual stocks' trends mixed in and if anything doesn't seem like a good candidate to try to cancel out.
L
Dear L,
Thank you again for thoughtful comments.
1. I used the Engle-Granger test for each component stock against XLE, and select the topN ones with the best t-stat.
Your idea of an out-of-sample test is a good one and I may produce one in the future. I did not include it here because this is not a complete trading strategy, just an idea that may interest some traders.
I am not sure about the point you made about "basically recover the index component structure". The whole exercise is to show that you don't need all N stocks to create a basket that cointegrates with the fund XLE -- and I don't want the "best" basket which you correctly pointed out compose of all XLE component stocks. With the best basket, there is no trading opportunity since there is little deviation!
2. I disagree with your assertion that there is no fundamental reason for the cointegration between a basket of component stocks with XLE. All the component stocks belong to the same economic sector, driven by the same factors. Meanwhile, XLE is supposed to represent the average performance of this sector. Maybe I am not understanding your argument correctly?
3. It is quite true that cointegration test can sometimes find a cointegration relation that does not hold up in out-of-sample test. When we pair-trade stocks or other financial instruments, the failure of the relationship in out-of-sample data is usually due to the fact that a company has changed its business model, management, etc. Or perhaps there is a buy-out offer or restructuring in the works. The way to cure this relationship break-down is to diversify: if you have a large number of cointegrating relationships, you would hope that many of them will survive out-of-sample. For a few sectors, I have demonstrated that this can be done ... maybe I will post the result of the test here in the future also. Going back to my XLE vs basket, it is also possible that a heavily-weighted individual stock inside or outside of the basket suddenly experienced the forementioned metamorphosis and caused the relationship to break down.
In general, I am curious as to what you think of using cointegration technique for pair-trading stocks? It would seem that if you don't believe in the XLE basket trade, you won't believe in pair trading stocks either.
Ernie
Ernie,
Thanks again for the follow up. My previous comment was kind of all over the place -- I will try to be more to the point this time.
By far, my largest critique of your cointegration procedure is this: when a cointegration vector is inferred from the past data, the procedure is completely silent about how long this cointegration relationship will last for in the future. In order to be practical, the cointegration relationship needs to stay valid for some time that's larger than the typical mean reversion halftime. There does not seem to be a way to know that for your XLE example.
I suggest the following test. You seem to be building your XLE basket based on daily data starting from 2001. That gives you 1000+ data points -- let's call this number K. Split this range into [1,X] and [X+1, K] for some X.
Do your basket building based on [1,X] but plot the residuals for the entire range [1, K]. It would be interesting to see a few such plots for various Ks. You are likely to discover this: inside [1, X] things look good, Dickey-Fuller values look encouraging, the residuals are visually quite mean-reverting, etc etc. However, as soon as you cross X (i.e, go into the out-of-sample range), you will lose much of that mean reversion.
This happens for many different values of X, proving that cointegration is not lost simply because of "changes in business model, management" etc.
The fact is, the regression/least squared error minimization inherent in Engle-Granger and other fitting techniques *induces* some mean reversion purely by construction. Minimizing residuals will make them somewhat stationary over the training data period -- and a stationary series fitted to an ARMA-like model will necessarily appear to have mean reversion (stationarity implies mean reversion for an ARMA model). As soon as you go outside the sample, this mean reversion is no longer there. This is very much like the known spurious correlation phenomenon for a pair of random walk processes.
Does this make any sense? I am basically saying that out of sample, your XLE basket might look a lot less cointegrating with XLE than in sample.
How does this relate to the original issue of XLE being an index? If you want a cointegrating basket vector that's guaranteed to stay valid in the future, it will be the vector of component weights with which the index has been built. That's because there are market participants making sure there are no riskless arbitrage opportunities for XLE...
L,
Please see my latest post on out-of-sample testing.
Ernie
Hi Ernie,
I have a question regarding the graph of the spread on the posting: how you created the spread between 1000 shares of XLE vs 1000 units of basket? Can you also shed some light on how to interpret the graph?
Hi Anonymous,
The spread is simply defined as 1000*close price of XLE - 1000*close price of basket. The basket composition is given in my Premium Content site.
Ernie
Hi Ernest
The idea of trading baskets against a security is very interesting.
I was wondering if you had any thoughts on how one might approach the issue with FX pairs.
Would you make a basket of say the USD based pairs (excluding say AUD/USD) and then trade AUD/USD against the basket - subject to cointegration?
Curious....
Hi Anonymous,
If you believe that AUD cointegrates with a basket of currencies, then yes, your trade makes sense.
Ernie
Hi Ernest,
I am still unable to resolve the paradox brought up by the reader "L."
Let's say the ETF has N components, and you take a smaller subset n to form your baskets. And let's call the other components NOT in the basket e for error.
Since cointegration requires a linear combination of two time series to be stationary, you would run cointegration test on the ETF itself and the basket of n stocks. If cointegration does exist, that would mean that the time series of ETF - n stocks(a linear combination, I ignored the constant) is stationary, which will imply that the time series e(=N-n) is also stationary.
First of all, I don't see how e, being just stocks, can be stationary.
Secondly and more importantly, if e turns out to be stationary for whatever reason, why not just trade e instead of a probably more costly combination of ETF and the basket?
I am not sure if weights matter in this argument since e is simply just a "linear combination" of the ETF and the basket.
I will appreciate your comment.
Hi ezbentley,
I stand by my argument that relative weights of the components are important to whether a basket cointegrates with an index, contrary to what you argued.
The N-1 stock basket can cointegrate with an index, but the 1 stock basket will not, because in the 1 stock basket, that stock suddenly has weight of 1.
Ernie
Ernest,
Firstly, I thoroughly enjoyed reading your recent book on quant trading.
A question with regards to the half-life concept above. I'm attempting to implement and intraday index arb strategy, thus I would need to construct a basket with a much shorter half-life. My guess would be that I would actually want to take the 10 most correlated stocks in the index as they should mean-revert quicker than less correlated stocks in the index. I would appreciate your insights on this, my email is: ozel.christo AT gmail.com, thanks!
Anonymous,
Thanks for your kind words.
Yes, the more stocks you include in a basket, the shorter the half-life of mean-reversion to the corresponding ETF. However, it also implies smaller returns since cointegration is likely to be very tight. It may be a good candidate for high frequency trading.
Ernie
Ernest,
I thoroughly enjoyed your book, but I would like to bring up my issues with this strategy.
If I can again bring up the example of trading a basket of N-1 stocks against an index with N components. The deviations of your basket from the index will be due to the component that you have NOT included in your basket, say component X. I accept that the spread between the index and your basket will be stationary because the component X is in the same sector.
The problem that I can't put aside is the chance that the one component that we didn't include in our basket goes through an M&A. I can imagine myself waking up one day to the news that component X is merging with component Y (the leader) and its share price is about to open at a price that will wipe out all of my profits for the last year. This is something that your backtests and cointegration tests will not prepare you for. In your book you discuss the illogicality of using stop losses with mean reversion strategies (which I totally agree with), but at least stop losses put a limit on the amount of money you can lose on any one trade.
To sum up, I just think that this strategy lacks some serious risk management. The example is also quite conservative given that you trade a basket of 10 stocks in 33, leaving 23 component X's to stress about.
Jeff
Ernest,
Firstly, great book, it has become an important reference for me especially now as I'm attempting to construct a successful ETF pair strategy.
Just 2 questions:
a) I found it surprising that your basket of 10 stocks that a mean reversion time of 20 days. Considering that XLE only has 40 constituents, intuitively I would think that if you use the top 10 cointegrating stocks, your half-life would be much shorter, to be useful intraday even. My question is, if I'm looking to stat arb intraday, about how many stocks should I be including and/or how highly co-integrated should this basket be with the index?
b) In your book you give an example of how to find the hedge ratio in a pair trade in matlab. If I'm using excel, I'm wondering if this is equivalent to doing a linear regression and using the coefficients as the hedge ratio?
Thanks!
Anonymous,
Thanks for your kind words on my book.
a) Certainly the more stocks you include in your basket, the shorter the half-life. The number of stocks to include depends on your desired holding period. You can backtest the strategy to find that out.
b) Yes, hedge ratio is the coefficient from a linear regression.
Ernie
Hi Ernie,
I had a question regarding your statement that you can boost this return by using options to implement the XLE position. Is this always true for one side of the cointegrating pair? Could we also substitute options for stocks on both sides of a pair?
I didn't think that a cointegration test for equities would also translate into a strategy for options. I thought cointegration tells us about a linear combination of two stock prices while options are bets on individual stock prices.
Thanks
Hi Ernie -
What commission structure at IB are you working with? The retail commission structure is about 0.01 per share round trip so I am wondering whether these ETF/basket arb strategies work on that commission structure.
I have found a basket of 3 components that is cointegrated with an ETF with the spread oscillating between $1 and -$1. However my regression leads to the following hedge ratio:
ETF = 1
component_1 = 0.4418
component_2 = 1.622
component_3 = 0.2292
Should I the sum of the hedge ratio on the component side equal 1? I see from your graph of XLE you show 1000 units of XLE versus the same units of the basket.
Also - do you think the spread deviation that I have found is too narrow to profit on a retail level? Perhaps I need to find a weaker cointegration to increase profit potential.
I greatly appreciate your feedback.
Hi Anon,
IB's commission is about 0.5 cent per share, and can be lower for large volume.
You can scale your components and the ETF by any amount you like so as to trade round lots.
$1 stddev seems pretty reasonable.
Ernie
Hi Ernie - great job with the blog.
I had a simple question for you.
When you run the cointegration tests what lag should you use? I've been doing a lot of reading about this and its quite debatable. Mean reversion occurs at various time frequencies i.e. minutes, hours, days, weeks, months. So in that sense one could test using various different lags - no? I notice in some of your comments you use a lag=0. I would greatly appreciate some guidance on this issue as it would help me greatly.
Kind Regards,
Sam
Hi Anon,
There are 2 different use of the word "lag".
If you mean the lag used as a parameter in the cadf test, then I believe the result is not very sensitive to whether you use lag=0, 1, or 2.
However, I think you actually mean "lookback", which is the length of the data set used for the cadf test. In this case, it should be at least 1 year, but 3 years is ideal.
Ernie
Using linear/ridge regression to generate the ratio of a basket of stock means the mean square error of basket of stock and the index is minimized.
However, the target function should be maximizing the spread volatility while minimizing the convergence time.
Are there any study or paper regarding this topics?
Thank you(Joe bottleneck56 at gmail.com)
Joe,
I am not sure how you can have an objective function that does two things at once (maximize volatility AND minimize convergence time). At most, you can use one criterion as a constraint (fixed to a value), and use the other as objective.
Ernie
So if I keep the volatility fixed and minimize the convergence time or vice versa, do you think this object function will outperforms linear regression?
Are there any paper about this topics?
Thank you
bottleneck56 at gmail.com
Joe,
It may. No one can tell in advance, and you should just run the experiment yourself. I haven't seen any papers on this technique of find the best basket either.
Ernie
1. In co integration relationship for pairs trading, we regress S1 ~ S2 without intercept. But we know, regression without intercept increases R square dramatically.
How to handle this? R square change dramatically, how can we say that this fitting is not spurious?
2.We know, in non stationary time series, R square is not a good measure to check the goodness of fit. What measure I should use for regression equation provided we do not use constant in regression equation
Jeet,
Ultimately, you should see the Sharpe ratio of your strategy, irrespective of with R square you get for linear regression.
Often, a poor fit can still result in a profitable strategy.
Ernie
How would this process differ if you wanted to create a basket of goods to pairs trade against a single security with the constraint that basket cannot contain the security in which you want to trade individually? Would you have to come up with a factor model and run a PCA to discover underlying factors that drive correlation?
-NT
NT,
The process is the same for any basket, even if you impose the exclusion constraint. You don't need factor or PCA models.
Ernie
Hi Ernie,
Love your blog. I have a question. If one has restrictions on their trading such that they must hold positions for at least a week, would trading a basket of underlying symbols against their ETF still be a profitable strategy, in general?
It could still be profitable if the basket does not exactly replicate the ETF.
Ernie
Hi,
I'm following your code IndexArb.m (pg. 97-98 book "Algorithmic Trading:winning strategies..."
I'm using Matlab 2016 so I had to change ONLY the code line about johansen test.
I've followed the same model you suggested (include intercept but no trend and lags=1).
So I substituted your code : "results=johansen(y2, 0, 1); with this:
"[h,pValue,stat,cValue,mles]=jcitest(y2, 'model', 'H1*','lags',1);
Unfortunately, unlike your results (98 stocks cointegrated with the ETF) I never find a single stock cointegrated with it. It was so strange that I tested every johansen test model .
Nothing changed but...the quadratic trend model gave me 290 stocks cointegrated!.
But it's clear that something is wrong. I'm sure I'm using the very same time series "inputDataOHLCDaily_stocks_20120424" and "inputData_ETF" as well as the same training date you selected. I mean from 98 to 0 is something that worries me....
Beppe
Hi Beppe,
Again, this has nothing to do with the version of Matlab you are using. You need to download and install the free package from spatial-econometrics.com and use the johansen function there in order to get identical results as mine.
Ernie
Post a Comment