Maximizing growth without risking bankruptcy
Many hedge fund disasters come not from making the wrong bets – that happen to the best of us – but from making too big a bet by overleveraging. On the other hand, without using leverage (i.e. borrowing on margin to buy stocks), we often cannot realize the full growth potential of our investment strategy. So how much leverage should you use?
Surprisingly, the answer is well-known, but little practiced. It is called the Kelly criterion, named after a mathematician at Bell Labs. The leverage f is defined as the ratio of the size of your portfolio to your equity. Kelly criterion says: f should equal the expected excess return of the strategy divided by the expected variance of the excess return, or
f = (m-r)/s2
(The excess return being the return m minus the risk-free rate r.)
This quantity f looks like the familiar Sharpe ratio, but it is not, since the denominator is s2, not s as in the Sharpe ratio. However, if you can estimate the Sharpe ratio, say, from some backtest results of a strategy, you can also estimate f just as easily. Suppose I have a strategy with expected return of 12% over a period with risk-free rate being 4%. Also, let’s say the expected Sharpe ratio is 1. It is easy to calculate f, which comes out to be 12.5.
This is a shocking number. This is telling you that for this strategy, you should be leveraging your equity 12.5 times! If you have $100,000 in cash to invest, and if you really believe the expected values of your returns and Sharpe ratio, you should borrow money to trade a $1.2 million portfolio!
Of course, estimates of expected returns and Sharpe ratio are notoriously over-optimistic, what with the inevitable data-snooping bias and other usual pitfalls in backtesting strategies. The common recommendation is that you should halve your expected returns estimated from backtests when calculating f. This is often called the half-Kelly criterion. Still, in our example, the recommended leverage comes to 6.25 after halving the expected returns.
Fixing the leverage of a portfolio is not as easy or intuitive as it sounds. Back to our $100,000 example. Say you followed the (half-) Kelly criterion and bought a portfolio worth $625,000 with some borrowed money. The next day, disaster struck, and you lost 5%, or $31,250, of the value of your portfolio. So now your portfolio is worth only $593,750, and your equity is now only $68,750. What should you do? Most people I know will just stick to their guns and do nothing, hoping that the strategy will “recover”. But that’s not what the Kelly criterion would prescribe. Kelly says, if you want to avoid eventual bankruptcy (i.e. your equity going to zero or negative), you should immediately further reduce the size of your portfolio to $429,688. Why? Because the recommended leverage, 6.25, times your current equity, $68,750, is about $429,688.
Thus Kelly criterion requires you to sell into a loss (assuming you have a long-only portfolio here), and buys into a profit – something that requires steely discipline to achieve. It also runs counter to the usual mean-reversion expectation. But even if you strongly believe in mean-reversion, as no doubt many of the ruined hedge funds did, you need to consider protecting you and your investors from the possibility of bankruptcy before the market reverts.
Besides helping you to avoid bankruptcy, the Kelly criterion has another important mathematically proven property: it is a “growth-optimal” strategy. I.e. if your goal is to maximize your wealth (which equals your initial equity times the maximum growth rate possible using your strategy), Kelly criterion is the way.
Notice this goal is not the same as many hedge managers’ or their investors’ goal. They often want to maximize their Sharpe ratio, not growth rate, for the reason that their investors want to be able to redeem their shares at any time and be reasonably sure that they will redeem at a profit. Kelly criterion is not for such investors. If you adopt the Kelly criterion, there may be long periods of drawdown, highly volatile returns, low Sharpe ratio, and so forth. The only thing that Kelly guarantees (to an exponentially high degree of certainty), is that you will maximize the growth potential of your strategy in the long run, and you will not be bankrupt in the interim because of the inevitable short-term market fluctuations.
For further reading:
Poundstone, William. (2005). Fortune’s Formula. New York: Hill and Wang.
Thorp, Edward O. (1997; revised 1998). The Kelly Criterion in Blackjack, Sports Betting, and the Stock Market. www.bjmath.com/bjmath/thorp/paper.htm
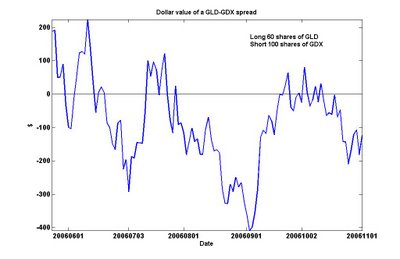
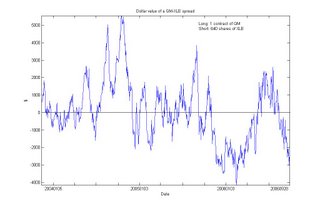
 This is not surprising. But does this imply the unsettling conclusion that the Canadian economy cointegrates with the emerging markets? No. I will not bore you with yet another chart: just be assured that cointegration is not a transitive relation.
This is not surprising. But does this imply the unsettling conclusion that the Canadian economy cointegrates with the emerging markets? No. I will not bore you with yet another chart: just be assured that cointegration is not a transitive relation.

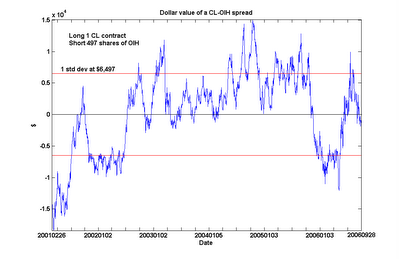
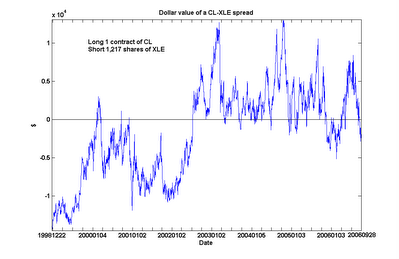 An interesting feature emerged from this extended analysis. CL and XLE are still found to be cointegrated over this long period, albeit with a slightly lower probability (90%). However, we can see something of a regime shift around mid-2002, when CL went from generally under-valued to over-valued relative to XLE. (Even after including this regime with lower relative crude oil prices in my calculations, I still find the current spread to be undervalued by about $10,521 as of the close of Nov 17, which is near its 6-year low.)
An interesting feature emerged from this extended analysis. CL and XLE are still found to be cointegrated over this long period, albeit with a slightly lower probability (90%). However, we can see something of a regime shift around mid-2002, when CL went from generally under-valued to over-valued relative to XLE. (Even after including this regime with lower relative crude oil prices in my calculations, I still find the current spread to be undervalued by about $10,521 as of the close of Nov 17, which is near its 6-year low.)



 Now consider stock A and stock C.
Now consider stock A and stock C. Stock C clearly doesn’t move in any correlated fashion with stock A: some days they move in same direction, other days opposite. Most days stock C doesn’t move at all! But notice that the spread in stock prices between C and A always return to about $1 after a while. This is a manifestation of cointegration between A and C. In this instance, a profitable trade would be to buy A and short C at around day 10, then exit both positions at around day 19. Another profitable trade would be to buy C and short A at around day 31, then closing out the positions around day 40.
Stock C clearly doesn’t move in any correlated fashion with stock A: some days they move in same direction, other days opposite. Most days stock C doesn’t move at all! But notice that the spread in stock prices between C and A always return to about $1 after a while. This is a manifestation of cointegration between A and C. In this instance, a profitable trade would be to buy A and short C at around day 10, then exit both positions at around day 19. Another profitable trade would be to buy C and short A at around day 31, then closing out the positions around day 40.